从博弈论的角度分析诈唬(2):特殊情况中的期望回报 从博弈论的角度分析诈唬(2):特殊情况中的期望回报 第一篇文章请点击这里: 从博弈论的角度分析诈唬(1):什么情况下该诈唬 今天,我们要说的是第三

从博弈论的角度分析诈唬(2):特殊情况中的期望回报
第一篇文章请点击这里:
从博弈论的角度分析诈唬(1):什么情况下该诈唬
今天,我们要说的是第三点:
一些特殊情况下的期望回报下面两张表显示了特殊情况中的期望回报。
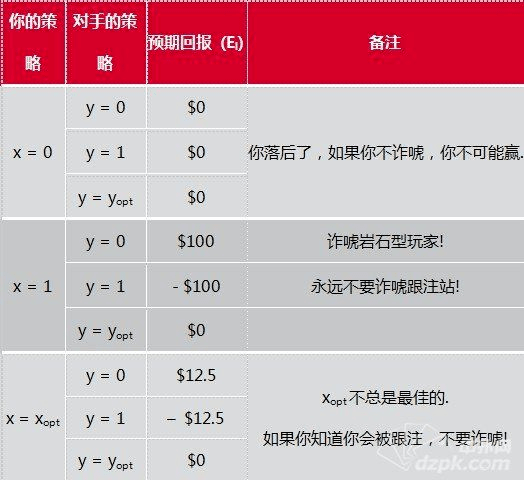
第一张图表示的是听牌失败时的期望回报,用上一篇文章的例子来计算:
对手的期望回报是你的期望回报的负数,再加上已经在底池中的$100。
他会得到你在下注轮的净损失+现有底池。当然如果你赢下底池的话,你的净损失是– $100,他没有回报。
来看看最简单的情况:当你的期望回报是0时,你的筹码量不会发生变化,因此你不会赢下底池,底池会被对手赢走。由于我们已经玩到河牌圈,所以这不是一个零和博弈。
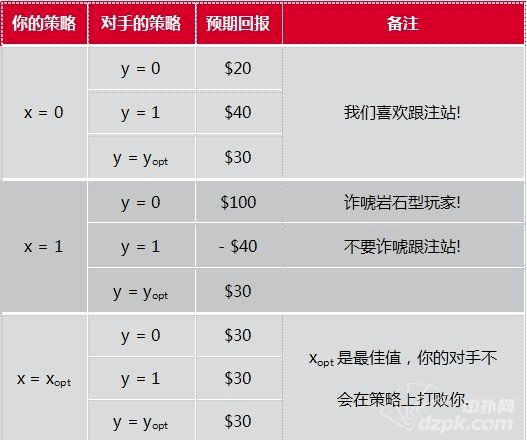
如果你知道什么时候诈唬,什么时候价值下注,而对手却不知道,对他来说(也可能是对你),下面的这个图表会更有用。
这张表显示的是综合获胜和失败之后,你的期望回报。我们假设过,你有20%的时候领先,80%的时候落后,因此你的平均期望回报是 qEw + (1 – q)El。(这个结果的负值+底池现有的$100=对手的期望回报Eop。)
结论当你面对优秀的对手时,最好的选择就是利用纳什均衡点为你提供的策略:xopt。在这种情况对手会用 yopt的策略打牌。如果他没有使用,他就在犯错(也说明他不是一个优秀的玩家),你就可以利用他的错误找到最佳的打法。
如果他经常跟注,你就少诈唬,如果他很少跟注,你就多诈唬。如果你能猜到他的跟注频率,就可以根据期望回报最大化的原则,计算自己应该诈唬的频率。
附录◆◆yopt是怎样计算的◆◆如果y = yopt,无论x是多少,你的期望回报都不会改变。让我们先假设x = 0,这时你什么牌也赢不了,公式是:
El = 0
现在假设x = 1,El的公式变为
El = (1 – yopt)P – yoptB
因为x=0和x=1时的期望回报一样,所以
(1 – yopt)P – yoptB = 0,
所以
(1 – yopt)P = yoptB,
P – yoptP = yoptB,
P = yopt(P + B),
最后
yopt = P/(P + B)
◆◆从对手的角度来看◆◆现在我们从对手的视角看看这个问题。
首先我们要列出他的期望回报Eop。由于他不知道你的牌是领先还是落后,所以他的期望回报还会受到q的影响,所以这个公式会复杂一点:
Eop = – qyB + q(1 – y)0 + (1 – q)xy(P + B) + x(1 – y)0 + (1 – x)P
– qyB 表示你有优胜牌,你下注,他跟注,并且输了。
q(1 – y)0表示你有优胜牌,但是他弃牌,没有输赢。
(1 – q)xy(P + B) + x(1 – y)0 + (1 – x)P是他领先时的情况。
方括号中xy(P + B)表示你诈唬,他跟注,他赢得底池和你的下注。
x(1 – y)0 表示你诈唬,他弃牌,没有盈利和损失。
(1 – x)P表示你弃牌,他赢下底池的情况(包括他过牌赢下摊牌和他下注你弃牌两种情况)
省略其中为0的部分,我们得到
Eop = (1 – q)xy(P + B) + (1 – x)P – qyB
如果对手知道你从不诈唬(x = 0),那他的最佳打法是什么?他永远不会跟注,在上面的公式中如果用0代替x,我们得到
Eop x=0 = (1 – q)P– qyB
为了使结果最大化,我们必须让y = 0 (永远不跟注)。
反过来,如果对手知道你总是诈唬(x = 1),那他就很难找到最佳应对方式了。如果x = 1,我们得到
Eop x=1 = (1 – q)y(P + B) – qyB = y(1 – q)(P + B) – qB
如果
(1 – q)(P + B) – qB > 0,
y = 1 (总是跟注)会让对手的期望回报最大化。
如果
(1 – q)(P + B) – qB < 0,
他就应该使用 y = 0 (永远不跟注)的策略。
(1 – q)(P + B) – qB < 0
意味着
(1 – q)(P + B) < qB,
P + B – qP – qB < qB,
P + B < q(P + 2B),
最后
q > (P + B)/(P + 2B)
在我们的例子中,P = B = $100,如果q > 2/3,对手应该永不跟注(即使他知道你总是下注;因此在这种情况中你总是应该诈唬), 当q < 2/3时,他应该总是跟注(如果他知道你总是诈唬)。记住,这个q的值也仅取决于底池大小和下注大小。
◆◆xopt是怎么计算的?◆◆如果x = xopt,那么无论y是多少,对手的期望回报都不会改变。和之前一样,先假设y = 0。Eop的公式为
Eop = (1 – q)(1 – xopt)P
现在假设y = 1,我们得到
Eop = (1 – q) xopt (P + B) + (1 – xopt)P – qB
因为y=0和y=1时的Eop一样,我们得到
(1 – q)(1 – xopt)P = (1 – q) xopt (P + B) + (1 – xopt)P – qB,
因此
qB = (1 – q) xopt (P + B)
(两边都有(1 – q)(1 – xopt)P,因此可以消掉),所以最终我们得到
xopt = qB/(1 – q)(P + B)
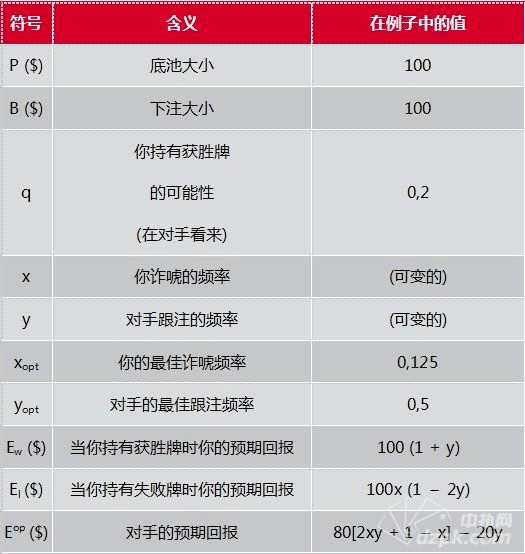
当我们讨论频率时,我们通常用 0.2代替20%,用0.5代替50%等等。一件不可能的事件发生的可能性是0 (0%),一件确定的事发生的可能性是1 (100%)。剩下的其他事件发生的可能性在0和1之间。https://www.moshike.com/
FAQ
吃瓜的好处?
什麼是「吃瓜群眾」? 吃的到底是什麼「瓜」? 已經成為網路慣用語的「吃瓜群眾」,指的是那些在事件發生後事不關己、圍觀閒聊的群體,之後也衍生出「吃瓜」這個詞,專門用來指圍觀、看好戲、說閒話的行為。Feb 18, 2025
吃瓜是怎么来的?
该词源于2016年网络热词“不明真相的吃瓜群众”(或简写为“吃瓜群众”),更早则来自百度贴吧中“前排出售瓜子”、“吃瓜子看戏”等用语,而“不明真相”是网民用来反讽中国官方话语中常见的“少数别有用心”、“不明真相的群众”等固定短语。
抖音短剧下载全攻略
抖音短剧真的超级火,但有时候想离线观看或者保存下来,怎么操作呢?其实最简单的方法就是用抖音自带的下载功能。只要打开抖音APP,找到喜欢的短剧,点右下角的“分享”按钮,再选择“保存视频”,视频就会自动存到手机相册。注意哦,有些视频可能因为版权限制不能下载,这种情况就需要换个方法啦。
遇到不能直接保存的短剧,别担心!可以试试第三方下载工具。比如“抖音视频下载器”或“快抖下载器”,这些软件能帮你通过复制视频链接,快速下载高质量的短剧。有些工具还能批量下载,比如你想一次性收藏一个作者所有短剧,轻松搞定。不过选下载软件时要小心,最好选正规平台,免得手机中毒或者个人信息泄露。
要是在手机上实在不好操作,也可以用电脑下载。先复制短剧链接,在电脑浏览器访问支持抖音视频下载的网站,或者用像4k Video Downloader这样的软件,把链接粘贴进去,一键下载。这样下载的视频质量通常很好,保存也方便。对上班族来说,工作间隙下载喜欢的短剧,晚上回家慢慢看,超级舒服。
还有一种特别实用的办法,就是屏幕录制。虽然不是下载,但操作简单又实用。只需打开手机的录屏功能,然后播放你想保存的短剧,录完还能编辑一下,上传朋友圈也很方便。虽然录制视频可能有些瑕疵,但在没有下载权限时,这招真心好用。
最后提醒一下,如果想下载大陆地区抖音短剧,要注意有些内容只能在国内版APP看到。安卓用户可以下载大陸抖音的APK安装包,iPhone用户则需要切换App Store的地区到中国大陆,然后再下载抖音。这样才能畅快追剧,不用担心找不到资源。下载的同时,也别忘了尊重版权,合法使用视频资源哦!
微短剧是什么?
尽管叫法不同,本文探讨的短剧,更多是当下颇为流行的微短剧。 根据国家广电总局的定义,微短剧,全称为网络微短剧,是指“单集时长从几十秒到15分钟左右、有着相对明确的主题和主线、较为连续和完整的故事情节”的剧集。 这类形式此前更常见于长视频平台,如此前爆火的《招惹》《授她以柄》。Mar 15, 2024
三黑料是什么意思?
料:主要指银行卡账号、密码,持卡人身份证号及绑定手机号四大类信息(又称CVV四大件)。 内料:指境内卡的四大件。 外料:指境外卡的四大件。 轨道料:指通过改装POS机得到的银行卡信息,这种信息一般非常精准。
































